算法

复杂度

时间复杂度

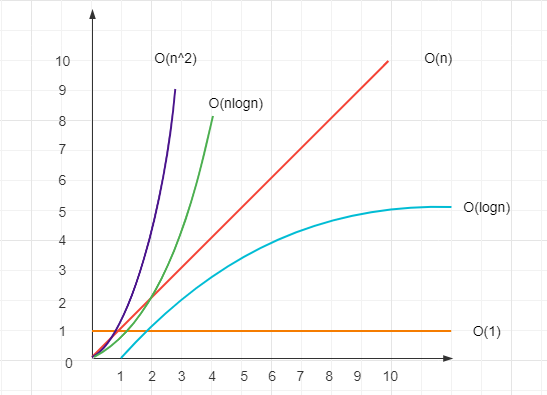
复杂度用 O 表示，说的是数量级，而不是具体的数字，如
- O(2) O(3) O(100) 其实都是 O(1)
- O(n) O(2 * n) 其实都是 O(n)
常见的时间复杂度
- O(1) 无循环
- O(n) 普通的循环
- O(logn) 有循环，但其中使用了二分法，例如：二分查找算法
- O(n*logn) 嵌套循环，一层是普通循环，一层有二分算法。例如：快速排序算法。
- O(n^2) 两个普通循环的嵌套，例如常见的冒泡排序。

空间复杂度

前端算法通常不太考虑空间复杂度，或者它比时间复杂度要次要的多。
因为前端环境，通常内存都是足够的，或者内存不够通常也是其他因素（如媒体文件）。

算法思维

贪心

贪心
- 贪心算法就是每一步都做当前看起来最优的选择，希望最终得到全局最优解。
- 它不考虑后续步骤的影响，只根据当前情况选择“最好”的选项。
示例：
- 找零钱问题：假设你要用最少的硬币凑出18元，硬币面额有5元、2元、1元。
- 贪心得做法：每次都先用面额最大的硬币，直到不能继续再用，剩余部分用次大面额硬币解决，依次类推。
- 过程：5 + 5 + 5 + 2 + 1 = 18，用了5个硬币。

二分

二分
- 二分法是一种高效查找方法，前提是数据是排好序的。
- 它每次比较目标值和中间值大小，缩小查找范围为一半，重复直到找到目标或范围为空。
例子
- 查找数字：在排序数组[1, 3, 5, 7, 9, 11]中查找7。
- 对比中间元素：第3个元素是7，刚好找到。
- 若中间没找到，判断目标和中间大小，决定搜索左半边还是右半边。

动态规划

动态规划
- 是一种通过把问题拆解为子问题，存储子问题结果避免重复计算，最终合成答案的算法。
- 适合有重叠子问题和最优子结构性质的问题。
- 把一个大问题，拆解为不同的小问题，递归向下（动态规划），再转换为循环来解决问题。
- 动态规划的核心思想是考虑最后一步的可能性，而不是考虑整个跳跃过程。
例子
- 斐波那契数列：fib(n) = fib(n-1) + fib(n-2)，前两个数为1。
- 直接递归会重复计算很多fib(小的值)；
- 动态规划会先计算并存储fib(1), fib(2)…，避免重复，效率大幅提升。

数据结构

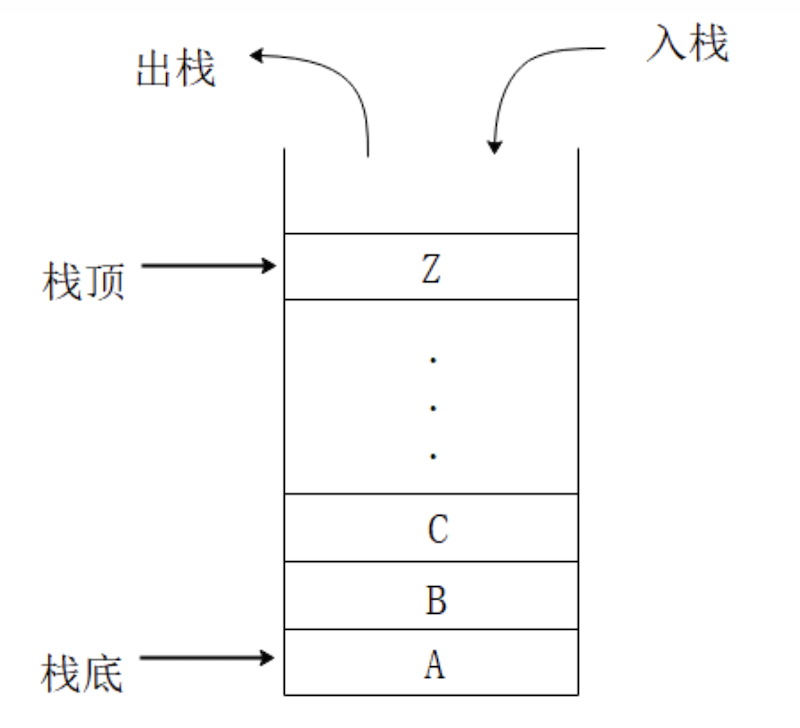
栈 Stack

先进后出
在 JS 中，栈一般情况下用数组实现：数组的push 和 pop 方法就是栈的体现（先进后出）

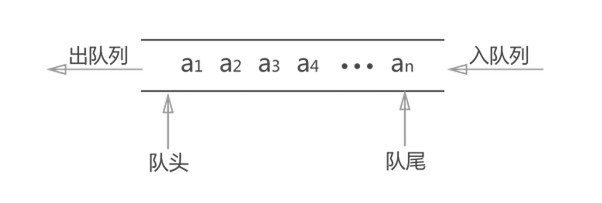
队列 Queue

先进先出
在 JS 中，使用数组的 push , unshift 队列的体现（先进先出）
- 但是考虑到数组的 unshift 方法，会导致数组的所有元素都要往后移动，增加复杂度
- 可是使用两个栈实现队列，就可以避免这个问题。

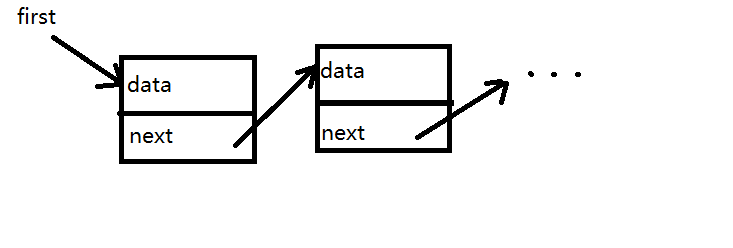
链表 Linked List

链表是一种物理结构（非逻辑结构），是数组的补充。
数组需要一段连续的内存空间，而链表不需要。
结构
- 单向链表 { value, next }
- 双向链表 { value, prev, next }
两者对比
- 链表：查询慢，新增和删除较快
- 数组：查询快，新增和删除较慢

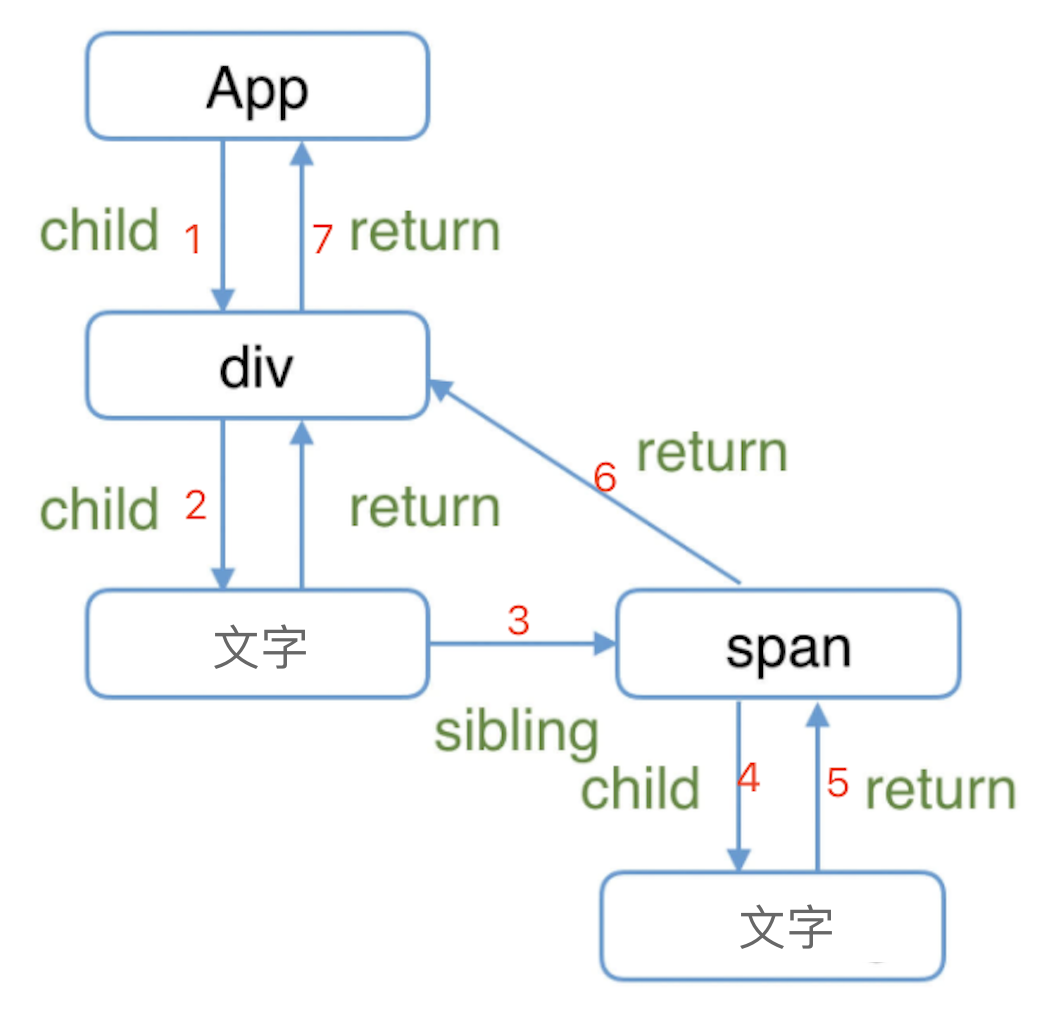
树

树
- 树，大家应该都知道，如前端常见的 DOM 树、vdom 结构。
二叉树
- 二叉树，顾名思义，就是每个节点最多能有两个子节点。
二叉树的遍历
- 前序遍历：root -> left -> right
- 中序遍历：left -> root -> right
- 后序遍历：left -> right -> root
高级二叉树
- 二叉搜索树 BST
  - 如果左右不平衡，也无法做到最优。
  - 极端情况下，它就成了链表 —— 这不是我们想要的。
- 平衡二叉搜索树 BBST ：
  - 要求树左右尽量平衡
  - 树高度 h 约等于 logn
  - 查找、增删，时间复杂度都等于 O(logn)
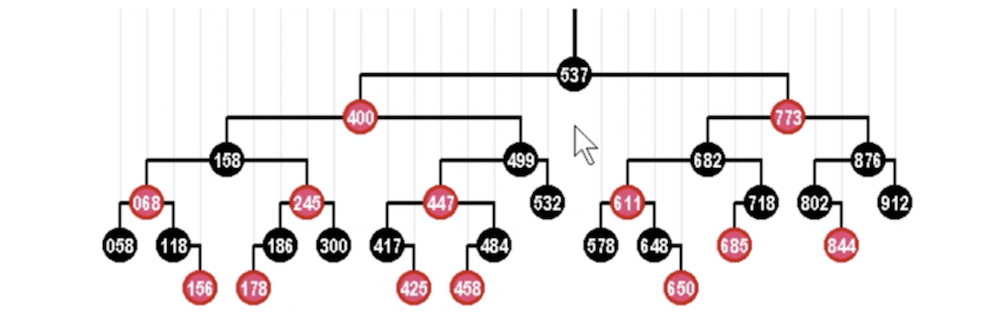
- 红黑树：
  - 一种自动平衡的二叉树
  - 节点分红/黑两种颜色，通过颜色转换来维持树的平衡
  - 相比于普通平衡二叉树，它维持平衡的效率更高
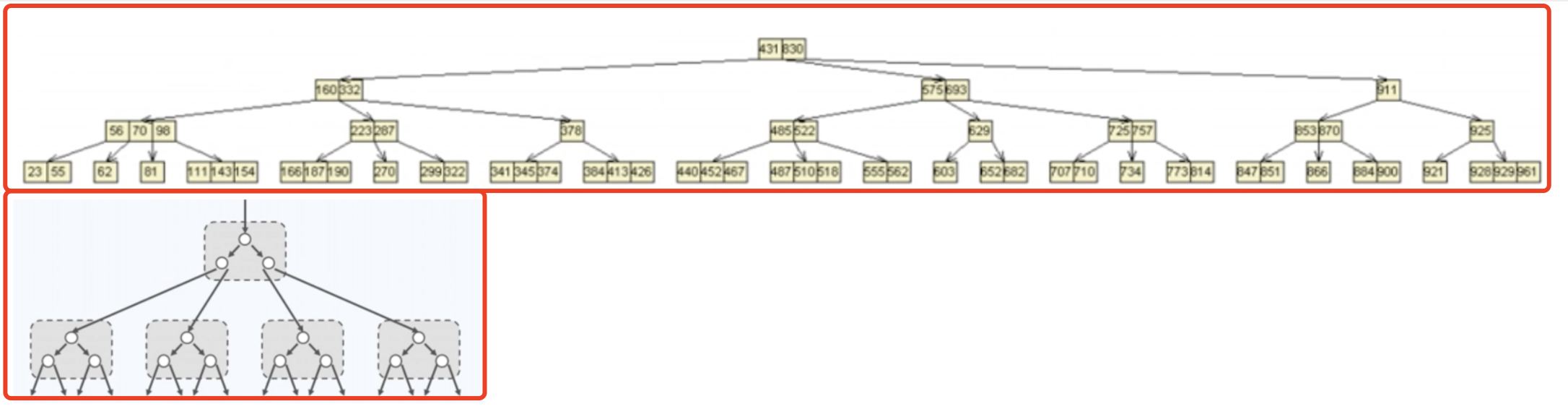
- B 树：
  - 物理上是多叉树，但逻辑上是一个 BST 。
  - 用于高效 I/O ，如关系型数据库就用 B 树来组织数据结构。

二叉搜索树 BST

特点：
- 左节点（包括其后代） <= 根节点
- 右节点（包括其后代） >= 根节点
优点
- 1、快速查找：
  - BST保证了节点按一定顺序排列：左子树节点的值都小于根节点，右子树节点的值都大于根节点
  - 查找某个元素时，不用遍历所有节点，而是通过比较值沿着树向左或向右子树递归查找，时间复杂度平均为 O(log n)，远快于链表的线性查找 O(n)。
- 2、动态数据结构，支持动态更新
  - BST支持动态插入和删除操作，且这些操作在平均情况下也能保持 O(log n) 的时间复杂度。相比于有序数组频繁插入删除代价高，BST更适合动态变化的数据。
- 3、有序遍历与排序
  - 对BST进行中序遍历，可以得到一个有序的序列。这使得BST可用于实现排序（例如树排序），并方便进行范围查询。
- 4、实现抽象数据类型
  - BST是实现集合（set）、映射（map）、优先队列等抽象数据结构的基础。它通过高效的查找、插入及删除保证操作的速度。
- 5、结构简单，易于理解和实现
  - 相较于哈希表等复杂数据结构，BST结构直观，通过递归实现非常方便，适合初学者理解树结构和递归算法。
总结：
- 通过保持节点有序，实现高效动态查找、插入和删除操作，是许多高效数据结构和算法的基础。
场景:
- 需要高效的元素查找、范围查询，比如：
  - 实现字典、映射（Map）
  - 数据库索引
  - 数据排序和动态集合操作
- 需要支持按键值区间遍历或查找特定区间元素
- 需要灵活插入、删除且保持顺序关系

堆

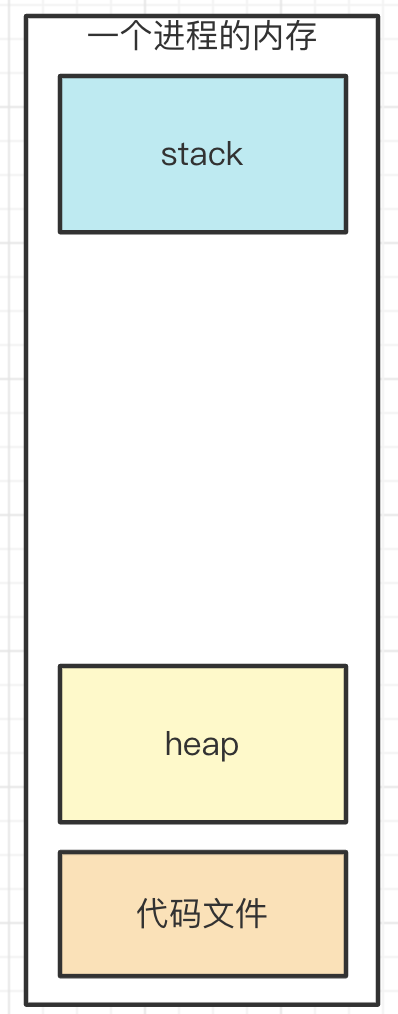
JS 执行时代码中的变量
- 值类型 - 存储到栈
- 引用类型 - 存储到堆
- 在 JavaScript 中，堆（Heap）是电脑中一块专门用来存放动态分配内存的区域，所有复杂数据类型（对象、数组、函数等）都是存放在这块堆的内存空间内。
堆的特点：
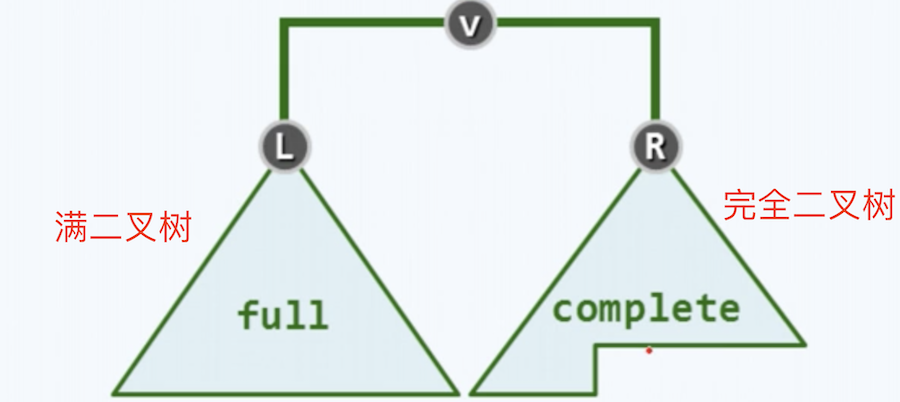
- 节点的值，总是不大于（或不小于）其父节点的值
- 完全二叉树（堆是一棵完全二叉树，即除了最后一层外，每层节点都被填满，且最后一层节点尽可能左对齐。）
- 堆就像一个大金字塔，每层都比下一层大（或小），顶端是最大（或最小）的宝石。这个结构方便我们快速找到最大或最小值。
- 堆用来帮你快速选出“最重要”的东西，比如任务优先级最高的。

堆，虽然逻辑上是二叉树，但实际上它使用数组来存储的。

// 上图是一个堆（从小到大），可以用数组表示
const heap = [-1, 10, 14, 25, 33, 81, 82, 99] // 忽略 0 节点
// 节点关系
const parentIndex = Math.floor(i / 2)
const leftIndex = 2 * i
const rightIndex = 2 * i + 1

堆的排序规则，没有 BST 那么严格，这就造成了
- 查询比 BST 慢
- 增删比 BST 快，维持平衡也更快
- 但整体复杂度都是 O(logn) 级别，即树的高度
但结合堆的应用场景
- 一般使用内存地址（栈中保存了）来查询，不会直接从根节点搜索（因为堆的物理结构是数组，所以查询复杂度就是 O(1)）
总结
- 物理结构是数组（空间更小），逻辑结构是二叉树（操作更快）
- 适用于“堆栈”结构
v8如何实现
- V8中的堆数据结构实现是这种物理上用数组存储，逻辑上表现为二叉树的经典设计模式、
- 用数组实现堆
  - 空间紧凑：数组是连续内存空间，比链式二叉树减少了额外指针开销，节省内存。
  - 索引计算简单：利用数组索引即可快速定位父节点和左右子节点，无需额外指针。
  - 数组映射成二叉树 父节点索引：Math.floor((i - 1) / 2) 左子节点索引：2 * i + 1 右子节点索引：2 * i + 2
- 插入（Insert）：
  - 先把元素放到数组末尾，模拟二叉树“最底层、最右端”添加节点。
  - 然后通过“上浮（bubble up）”操作，逐步和父节点比较并交换，维持堆的性质。
- 删除堆顶（Extract）：
  - 将根节点与数组末尾元素交换，删除末尾（原根节点）。
  - 然后通过“下沉（sink down）”操作，将新的根节点逐步和子节点比较并交换，恢复堆结构。

性能

数组：查找易，增删难（因为需要移动元素）
链表：增删易，查找难（因为需要遍历）
二叉搜索树 BST ：查找易，增删易（使用二分算法，将两者优点结合起来）

题目

旋转数组

题目
- 定义一个函数，实现数组的旋转。
- 如输入 [1, 2, 3, 4, 5, 6, 7] 和 key = 3，输出 [5, 6, 7, 1, 2, 3, 4]
思路1
- 将 k 后面的元素，挨个 pop 然后 unshift 到数组前面
思路2
- 将 k 后面的所有元素拿出来作为 part1
- 将 k 前面的所有元素拿出来作为 part2
- 返回 part1.concat(part2)
性能对比
- 时间复杂度
  - 思路1 - 看代码时间复杂度是 O(n)，但数组是有序结构 unshift 本身就是 O(n) 复杂度，所以实际复杂度是 O(n^2)
  - 思路2 - O(1)。slice 和 concat 不会修改原数组，而数组是有序结构，复杂度是 O(1) 。
- 空间复杂度
  - 思路1 - O(1)
  - 思路2 - O(n)

/**
 * 旋转数组 k 步 - 使用 pop 和 unshift
 * @param arr arr
 * @param k k
 * @returns arr
 */
export function rotate1(arr: number[], k: number): number[] {
    const length = arr.length
    if (!k || length === 0) return arr
    const step = Math.abs(k % length) // abs 取绝对值

    // O(n^2)
    for (let i = 0; i < step; i++) {
        const n = arr.pop()
        if (n != null) {
            arr.unshift(n) // 数组是一个有序结构，unshift 操作非常慢！！！ O(n)
        }
    }
    return arr
}

/**
 * 旋转数组 k 步 - 使用 concat
 * @param arr arr
 * @param k k
 */
 export function rotate2(arr: number[], k: number): number[] {
    const length = arr.length
    if (!k || length === 0) return arr
    const step = Math.abs(k % length) // abs 取绝对值

    // O(1)
    const part1 = arr.slice(-step) // O(1)
    const part2 = arr.slice(0, length - step)
    const part3 = part1.concat(part2)
    return part3
}

括号匹配

题目
- 一个字符串内部可能包含 { } ( ) [ ] 三种括号，判断该字符串是否是括号匹配的。
- 如 (a{b}c) 就是匹配的， {a(b 和 {a(b}c) 就是不匹配的。
思路
- 遇到左括号 { ( [ 则压栈
- 遇到右括号 } ) ] 则判断栈顶，相同的则出栈
- 最后判断栈 length 是否为 0

/**
 * @description 括号匹配
 */
/**
 * 判断左右括号是否匹配
 * @param left 左括号
 * @param right 右括号
 */
function isMatch(left: string, right: string): boolean {
    if (left === '{' && right === '}') return true
    if (left === '[' && right === ']') return true
    if (left === '(' && right === ')') return true
    return false
}
/**
 * 判断是否括号匹配
 * @param str str
 */
export function matchBracket(str: string): boolean {
    const length = str.length
    if (length === 0) return true
    const stack = []
    const leftSymbols = '{[('
    const rightSymbols = '}])'
    for (let i = 0; i < length; i++) {
        const s = str[i]
        if (leftSymbols.includes(s)) {
            // 左括号，压栈
            stack.push(s)
        } else if (rightSymbols.includes(s)) {
            // 右括号，判断栈顶（是否出栈）
            const top = stack[stack.length - 1]
            if (isMatch(top, s)) {
                stack.pop()
            } else {
                return false
            }
        }
    }

    return stack.length === 0
}

用两个栈实现一个队列

题目
- 请用两个栈，来实现队列的功能，实现功能 add delete length 。
思路
- 队列 add
  - 往 stack1 push 元素
- 队列 delete
  - 将 stack1 所有元素 pop 出来，push 到 stack2
  - 将 stack2 执行一次 pop
  - 再将 stack2 所有元素 pop 出来，push 进 stack1

/**
 * @description 两个栈 - 一个队列
 */
export class MyQueue {
    private stack1: number[] = []
    private stack2: number[] = []
    /**
     * 入队
     * @param n n
     */
    add(n: number) {
        this.stack1.push(n)
    }
    /**
     * 出队
     */
    delete(): number | null {
        let res
        const stack1 = this.stack1
        const stack2 = this.stack2
        // [1 2 3 4 5]
        // 将 stack1 所有元素移动到 stack2 中
        while(stack1.length) {
            const n = stack1.pop()
            // 5 4 3 2 1
            if (n != null) {
                // 5 4 3 2 1
                stack2.push(n)
            }
        }
        // stack2 pop 真正删除的地方
        res = stack2.pop() // 1
        // 将 stack2 所有元素“还给”stack1
        while(stack2.length) {
            const n = stack2.pop()
            // 2 3 4 5
            if (n != null) {
                stack1.push(n)
            }
        }
        return res || null
    }
    get length(): number {
        return this.stack1.length
    }
}

反转单向链表

题目
- 定义一个函数，输入一个单向链表的头节点，反转该链表，并输出反转之后的头节点
思路
- 至少要存储 3 个指针 prevNode curNode nextNode
性能对比
- 时间复杂度 O(n)

/**
 * @description 反转单向链表
 */
export interface ILinkListNode {
    value: number
    next?: ILinkListNode
}
/**
 * 反转单向链表，并返回反转之后的 head node
 * @param listNode list head node
 */
export function reverseLinkList(listNode: ILinkListNode): ILinkListNode {
    // 定义三个指针
    let prevNode: ILinkListNode | undefined = undefined
    let curNode: ILinkListNode | undefined = undefined
    let nextNode: ILinkListNode | undefined = listNode
    // 以 nextNode 为主，遍历链表
    while(nextNode) {
        // 第一个元素，删掉 next ，防止循环引用
        if (curNode && !prevNode) {
            delete curNode.next
        }
        // 反转指针
        if (curNode && prevNode) {
            curNode.next = prevNode
        }
        // 整体向后移动指针
        prevNode = curNode
        curNode = nextNode
        nextNode = nextNode?.next
    }
    // 最后一个的补充：当 nextNode 空时，此时 curNode 尚未设置 next
    curNode!.next = prevNode
    return curNode!
}

/**
 * 根据数组创建单向链表
 * @param arr number arr
 */
export function createLinkList(arr: number[]): ILinkListNode {
    const length = arr.length
    if (length === 0) throw new Error('arr is empty')
    let curNode: ILinkListNode = {
        value: arr[length - 1]
    }
    if (length === 1) return curNode
    for (let i = length - 2; i >= 0; i--) {
        curNode = {
            value: arr[i],
            next: curNode
        }
    }
    return curNode
}

const arr = [100, 200, 300, 400, 500]
const list = createLinkList(arr)
console.info('list:', list)

const list1 = reverseLinkList(list)
console.info('list1:', list1)

二分查找

题目
- 用 Javascript 实现二分查找（针对有序数组），说明它的时间复杂度
思路
- 递归 - 代码逻辑更加简洁
- 循环 - 性能更好（就调用一次函数，而递归需要调用很多次函数，创建函数作用域会消耗时间）
性能对比
- 时间复杂度 O(logn)

/**
 * @description 二分查找
 */
/**
 * 二分查找（循环）
 * @param arr arr
 * @param target target
 */
export function binarySearch1(arr: number[], target: number): number {
    const length = arr.length
    if (length === 0) return -1
    let startIndex = 0 // 开始位置
    let endIndex = length - 1 // 结束位置
    while (startIndex <= endIndex) {
        const midIndex = Math.floor((startIndex + endIndex) / 2)
        const midValue = arr[midIndex]
        if (target < midValue) {
            // 目标值较小，则继续在左侧查找
            endIndex = midIndex - 1
        } else if (target > midValue) {
            // 目标值较大，则继续在右侧查找
            startIndex = midIndex + 1
        } else {
            // 相等，返回
            return midIndex
        }
    }
    return -1
}
/**
 * 二分查找（递归）
 * @param arr arr
 * @param target target
 * @param startIndex start index
 * @param endIndex end index
 */
export function binarySearch2(arr: number[], target: number, startIndex?: number, endIndex?: number): number {
    const length = arr.length
    if (length === 0) return -1
    // 开始和结束的范围
    if (startIndex == null) startIndex = 0
    if (endIndex == null) endIndex = length - 1
    // 如果 start 和 end 相遇，则结束
    if (startIndex > endIndex) return -1
    // 中间位置
    const midIndex = Math.floor((startIndex + endIndex) / 2)
    const midValue = arr[midIndex]
    if (target < midValue) {
        // 目标值较小，则继续在左侧查找
        return binarySearch2(arr, target, startIndex, midIndex - 1)
    } else if (target > midValue) {
        // 目标值较大，则继续在右侧查找
        return binarySearch2(arr, target, midIndex + 1, endIndex)
    } else {
        // 相等，返回
        return midIndex
    }
}

两数之和

题目
- 输入一个递增的数字数组，和一个数字 n 。找出两个数之和等于 n 的两个数字。
- 例如输入 [1, 2, 4, 7, 11, 15] 和 15 ，返回两个数 [4, 11]
题目的要点
- 递增，从小打大排序
- 只需要两个数字，而不是多个
思路一：常规思路
- 嵌套循环，找个一个数，然后再遍历剩余的数，求和，判断。
- 时间复杂度 O(n^2) ，基本不可用。
思路2：利用递增的特性
- 数组是递增的
  - 随便找两个数
  - 如果和大于 n ，则需要向前寻找
  - 如果和小于 n ，则需要向后寻找 —— 二分法
- 双指针（指针就是索引，如数组的 index）
  - i 指向头，j 指向尾，求 i + j 的和
  - 和如果大于 n ，则说明需要减少，则 j 向前移动（递增特性）
  - 和如果小于 n ，则说明需要增加，则 i 向后移动（递增特性）
性能对比
- 思路1：时间复杂度 O(n^2)
- 思路1：时间复杂度降低到 O(n)

/**
 * @description 两数之和
 */
/**
 * 寻找和为 n 的两个数（嵌套循环）
 * @param arr arr
 * @param n n
 */
export function findTowNumbers1(arr: number[], n: number): number[] {
    const res: number[] = []
    const length = arr.length
    if (length === 0) return res
    // O(n^2)
    for (let i = 0; i < length - 1; i++) {
        const n1 = arr[i]
        let flag = false // 是否得到了结果
        for (let j = i + 1; j < length; j++) {
            const n2 = arr[j]
            if (n1 + n2 === n) {
                res.push(n1)
                res.push(n2)
                flag = true
                break
            }
        }
        if (flag) break
    }
    return res
}
/**
 * 查找和为 n 的两个数（双指针）
 * @param arr arr
 * @param n n
 */
export function findTowNumbers2(arr: number[], n: number): number[] {
    const res: number[] = []
    const length = arr.length
    if (length === 0) return res
    let i = 0 // 头
    let j = length - 1 // 尾
    // O(n)
    while (i < j) {
        const n1 = arr[i]
        const n2 = arr[j]
        const sum = n1 + n2
        if (sum > n) {
            // sum 大于 n ，则 j 要向前移动
            j--
        } else if (sum < n) {
            // sum 小于 n ，则 i 要向后移动
            i++
        } else {
            // 相等
            res.push(n1)
            res.push(n2)
            break
        }
    }
    return res
}
// 功能测试
const arr = [1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2,1, 2, 4, 7, 11, 15]
// console.info(findTowNumbers2(arr, 15))
console.time('findTowNumbers1')
for (let i = 0; i < 100 * 10000; i++) {
    findTowNumbers1(arr, 15)
}
console.timeEnd('findTowNumbers1') // 730ms
console.time('findTowNumbers2')
for (let i = 0; i < 100 * 10000; i++) {
    findTowNumbers2(arr, 15)
}
console.timeEnd('findTowNumbers2') // 102

求二叉搜索树的第 K 小的值

题目
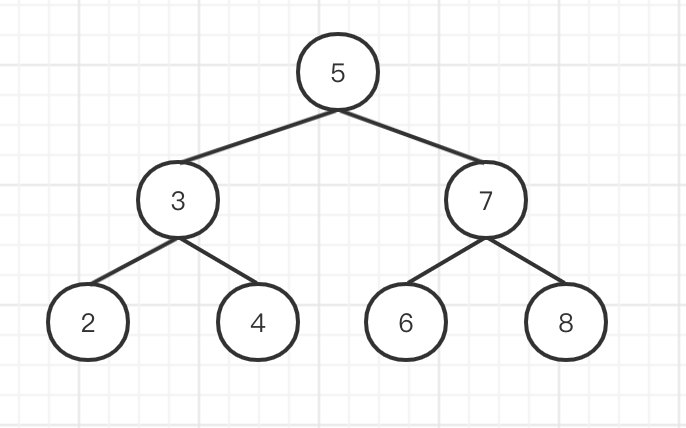
- 一个二叉搜索树，求其中的第 K 小的节点的值。
- 如下图，第 3 小的节点是 4

思路
- 分析题目
  - 根据 BST 的特点，中序遍历的结果，正好是按照从小到大排序的结果。
  - 所以，中序遍历，求数组的 arr[k] 即可。

/**
 * @description 二叉搜索树
 */
export interface ITreeNode {
    value: number
    left: ITreeNode | null
    right: ITreeNode | null
}
const arr: number[] = []
/**
 * 二叉树前序遍历
 * @param node tree node
 */
function preOrderTraverse(node: ITreeNode | null) {
    if (node == null) return
    // console.log(node.value)
    arr.push(node.value)
    preOrderTraverse(node.left)
    preOrderTraverse(node.right)
}
/**
 * 二叉树中序遍历
 * @param node tree node
 */
function inOrderTraverse(node: ITreeNode | null) {
    if (node == null) return
    inOrderTraverse(node.left)
    // console.log(node.value)
    arr.push(node.value)
    inOrderTraverse(node.right)
}
/**
 * 二叉树后序遍历
 * @param node tree node
 */
function postOrderTraverse(node: ITreeNode | null) {
    if (node == null) return
    postOrderTraverse(node.left)
    postOrderTraverse(node.right)
    // console.log(node.value)
    arr.push(node.value)
}
/**
 * 寻找 BST 里的第 K 小值
 * @param node tree node
 * @param k 第几个值
 */
export function getKthValue(node: ITreeNode, k: number): number | null {
    inOrderTraverse(node)
    return arr[k - 1] || null
}
const bst: ITreeNode = {
    value: 5,
    left: {
        value: 3,
        left: {
            value: 2,
            left: null,
            right: null
        },
        right: {
            value: 4,
            left: null,
            right: null,
        }
    },
    right: {
        value: 7,
        left: {
            value: 6,
            left: null,
            right: null
        },
        right: {
            value: 8,
            left: null,
            right: null
        }
    }
}
// preOrderTraverse(bst)
// inOrderTraverse(bst)
// postOrderTraverse(bst)
console.log(getKthValue(bst, 3))

斐波那契数列 &I

题目
- 用 Javascript 计算第 n 个斐波那契数列的值，注意时间复杂度。
思路
- 分析
  - 斐波那契数列很好理解
  - f(0) = 0
  - f(1) = 1
  - f(n) = f(n - 1) + f(n - 2) 前两个值的和
- 思路1：递归计算
  - 但这种方式会导致很多重复计算。
  - 时间复杂度是 O(2^n) ，爆炸式增长，不可用。（可以试试 n: 100 ，程序会卡死）
- 思路2：循环
  - 不用递归，用循环，记录中间结果。时间复杂度降低到 O(n)
性能对比
- 思路1：时间复杂度 O(2^n)
- 思路2：时间复杂度 O(n)

/**
 * @description 斐波那契数列
 */
// /**
//  * 斐波那契数列（递归）
//  * @param n n
//  */
// function fibonacci(n: number): number {
//     if (n <= 0) return 0
//     if (n === 1) return 1

//     return fibonacci(n - 1) + fibonacci(n - 2)
// }
/**
 * 斐波那契数列（循环）
 * @param n n
 */
export function fibonacci(n: number): number {
    if (n <= 0) return 0
    if (n === 1) return 1

    let n1 = 1 // 记录 n-1 的结果
    let n2 = 0 // 记录 n-2 的结果
    let res = 0

    for (let i = 2; i <= n; i++) {
        res = n1 + n2

        // 记录中间结果
        n2 = n1
        n1 = res
    }
    return res
}
// 功能测试
// console.log(fibonacci(10))

青蛙跳台阶

题目
- 一只青蛙，一次可以跳 1 个台阶，也可以跳 2 个台阶，问该青蛙跳上 n 级台阶，总共有多少种方式？
思路1：递归
- f(1) = 1 跳 1 级台阶，只有一种方式
- f(2) = 2 跳 2 级台阶，有两种方式
- f(n) = f(n - 1) + fn(n - 2) 跳 n 级，可拆分为两个问题
  - 第一次跳，要么 1 级，要么 2 级，只有这两种
  - 第一次跳 1 级，剩下有 f(n - 1) 种方式
  - 第一次跳 2 级，剩下有 f(n - 2) 种方式
思路2：动态规划
- 青蛙要跳上第 i 级台阶，有两种可能：
  - 从第 i-1 级台阶跳 1 级上来。
  - 从第 i-2 级台阶跳 2 级上来。
  - 两种方式是互斥的：指的是最后一步只能选择一种跳法 (从 n-1 跳 1 步，或者从 n-2 跳 2 步)
- 因此，跳上第 i 级台阶的总跳法数等于跳上第 i-1 级台阶的跳法数加上跳上第 i-2 级台阶的跳法数。
- 动态规划的核心思想是考虑最后一步的可能性，而不是考虑整个跳跃过程。

/**
 * 计算青蛙跳上 n 级台阶的总方式数 (优化空间复杂度)
 *
 * @param {number} n 台阶数
 * @returns {number} 总方式数
 */
export function frogJump1(n:number) {
    if (n <= 1) {
      return 1;
    }

    let a = 1; // dp[0]：跳上 0 级台阶的跳法数
    let b = 1; // dp[1]：跳上 1 级台阶的跳法数
    let result = 0; // 用于保存 dp[i]

    for (let i = 2; i <= n; i++) {
      result = a + b; // dp[i] = dp[i-1] + dp[i-2]
      a = b; // 更新 dp[i-2] 为 dp[i-1]
      b = result; // 更新 dp[i-1] 为 dp[i]
    }

    return result; // 返回 dp[n]
  }
export function frogJump2(n:number) {
    if (n <= 1) {
      return 1;
    }

    const dp = new Array(n + 1);
    dp[0] = 1;
    dp[1] = 1;

    for (let i = 2; i <= n; i++) {
      dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
  }

移动 0

题目
- 定义一个函数，将数组种所有的 0 都移动到末尾，例如输入 [1, 0, 3, 0, 11, 0] 输出 [1, 3, 11, 0, 0, 0]。
- 要求： 只移动 0 ，其他数字顺序不变 考虑时间复杂度 必须在原数组就行操作
思路1：非原数组操作
- 定义 part1 part2 两个空数组
- 遍历数组，非 0 push 到 part1 ，0 push 到 part2
- 返回 part1.concat(part2)
- 所以，遇到类似问题，要提前问面试官：是否能在原数组基础上修改？
思路2：原数组操作
- 遍历数组
- 遇到 0 则 push 到数组末尾
- 然后用 splice 截取掉当前元素
思路3：双指针
- 指针1 指向第一个 0 ，指针2 指向第一个非 0
- 把指针1 和指针2 进行交换
- 指针向后移
分析性能
- 思路1：非原数组操作
  - 时间复杂度 O(n) 空间复杂度 O(n) ，
- 思路2：原数组操作
  - 空间复杂度没有问题 O(1)
  - 时间复杂度：看似是 O(n)
  - 但实际上 splice 和 unshift 一样，修改数组结构，时间复杂度是 O(n)
  - 总体看来时间复杂度是 O(n^2)，不可用
- 思路3：双指针
  - 时间复杂度 O(n)
  - 空间复杂度 O(1)

/**
 * @description 移动 0 到数组末尾
 */
/**
 * 移动 0 到数组的末尾（嵌套循环）
 * @param arr number arr
 */
export function moveZero1(arr: number[]): void {
    const length = arr.length
    if (length === 0) return

    let zeroLength = 0

    // O(n^2)
    for (let i = 0; i < length - zeroLength; i++) {
        if (arr[i] === 0) {
            arr.push(0)
            arr.splice(i, 1) // 本身就有 O(n)
            i-- // 数组截取了一个元素，i 要递减，否则连续 0 就会有错误
            zeroLength++ // 累加 0 的长度
        }
    }
}

/**
 * 移动 0 到数组末尾（双指针）
 * @param arr number arr
 */
export function moveZero2(arr: number[]): void {
    const length = arr.length
    if (length === 0) return

    let i
    let j = -1 // 指向第一个 0
    for (i = 0; i < length; i++) {
        if (arr[i] === 0) {
            // 在数组中找到第一个 0 的位置，初始给 j
            if (j < 0) {
                j = i
            }
        }

        if (arr[i] !== 0 && j >= 0) {
            // 找到不是0的元素，并且也找到 0的元素，进行交换
            const n = arr[i]
            arr[i] = arr[j]
            arr[j] = n

            j++
        }
    }
}

// // 功能测试
// const arr = [1, 0, 3, 4, 0, 0, 11, 0]
// moveZero2(arr)
// console.log(arr)

// const arr1 = []
// for (let i = 0; i < 20 * 10000; i++) {
//     if (i % 10 === 0) {
//         arr1.push(0)
//     } else {
//         arr1.push(i)
//     }
// }
// console.time('moveZero1')
// moveZero1(arr1)
// console.timeEnd('moveZero1') // 262ms

// const arr2 = []
// for (let i = 0; i < 20 * 10000; i++) {
//     if (i % 10 === 0) {
//         arr2.push(0)
//     } else {
//         arr2.push(i)
//     }
// }
// console.time('moveZero2')
// moveZero2(arr2)
// console.timeEnd('moveZero2') // 3ms

连续最多的字符

题目
- 给一个字符串，找出连续最多的字符，以及次数。
- 例如字符串 'aabbcccddeeee11223' 连续最多的是 e ，4 次。
思路1：传统方式
- 嵌套循环，找出每个字符的连续次数，并记录比较。
思路2：双指针
- 指针1 指向第一个字符，指针2 指向第二个字符
- 如果两个字符相同，则指针2 向后移
- 如果两个字符不同，则指针1 指向指针2 的位置，指针2 向后移
分析性能
- 思路1：时间复杂度看似是 O(n^2)，因为是嵌套循环。 但实际上它的时间复杂度是 O(n)，因为循环中有跳转。
- 思路2：
  - 时间复杂度 O(n)
  - 空间复杂度 O(1)

/**
 * @description 连续字符
 */

interface IRes {
    char: string
    length: number
}

/**
 * 求连续最多的字符和次数（嵌套循环）
 * @param str str
 */
export function findContinuousChar1(str: string): IRes {
    const res: IRes = {
        char: '',
        length: 0
    }

    const length = str.length
    if (length === 0) return res

    let tempLength = 0 // 临时记录当前连续字符的长度

    // O(n)
    for (let i = 0; i < length; i++) {
        tempLength = 0 // 重置

        for (let j = i; j < length; j++) {
            if (str[i] === str[j]) {
                tempLength++
            }

            if (str[i] !== str[j] || j === length - 1) {
                // 不相等，或者已经到了最后一个元素。要去判断最大值
                if (tempLength > res.length) {
                    res.char = str[i]
                    res.length = tempLength
                }

                if (i < length - 1) {
                    i = j - 1 // 跳步
                }

                break
            }
        }
    }

    return res
}

/**
 * 求连续最多的字符和次数（双指针）
 * @param str str 
 */
export function findContinuousChar2(str: string): IRes {
    const res: IRes = {
        char: '',
        length: 0
    }

    const length = str.length
    if (length === 0) return res

    let tempLength = 0 // 临时记录当前连续字符的长度
    let i = 0
    let j = 0

    // O(n)
    for (; i < length; i++) {
        if (str[i] === str[j]) {
            tempLength++
        }

        if (str[i] !== str[j] || i === length - 1) {
            // 不相等，或者 i 到了字符串的末尾
            if (tempLength > res.length) {
                res.char = str[j]
                res.length = tempLength
            }
            tempLength = 0 // reset

            if (i < length - 1) {
                j = i // 让 j “追上” i
                i-- // 细节
            }
        }
    }

    return res
 }

// // 功能测试
// const str = 'aabbcccddeeee11223'
// console.info(findContinuousChar2(str))

// let str = ''
// for (let i = 0; i < 100 * 10000; i++) {
//     str += i.toString()
// }

// console.time('findContinuousChar1')
// findContinuousChar1(str)
// console.timeEnd('findContinuousChar1') // 219ms

// console.time('findContinuousChar2')
// findContinuousChar2(str)
// console.timeEnd('findContinuousChar2') // 228ms

快速排序 &I

题目
- 用 Javascript 实现快速排序，并说明时间复杂度。
思路
- 快速排序是基础算法之一，算法思路是固定的
  - 找到中间位置 midValue
  - 遍历数组，小于 midValue 放在 left ，大于 midValue 放在 right
  - 继续递归，concat 拼接
- splice 和 slice
  - 代码实现时，获取 midValue 可以通过 splice 和 slice 两种方式
  - 理论分析，slice 要优于 splice ，因为 splice 会修改原数组。
  - 但实际性能测试发现两者接近。
  - 但是，即便如此还是倾向于选择 slice —— 因为它不会改动原数组，类似于函数式编程
性能分析
- 快速排序时间复杂度 O(n*logn) —— 有遍历，有二分
- 普通的排序算法（如冒泡排序）时间复杂度时 O(n^2)

/**
 * @description 快速排序
 */

/**
 * 快速排序（使用 splice）
 * @param arr number arr
 */
export function quickSort1(arr: number[]): number[] {
    const length = arr.length
    if (length === 0) return arr

    const midIndex = Math.floor(length / 2)
    const midValue = arr.splice(midIndex, 1)[0]

    const left: number[] = []
    const right: number[] = []

    // 注意：这里不用直接用 length ，而是用 arr.length 。因为 arr 已经被 splice 给修改了
    for (let i = 0; i < arr.length; i++) {
        const n = arr[i]
        if (n < midValue) {
            // 小于 midValue ，则放在 left
            left.push(n)
        } else {
            // 大于 midValue ，则放在 right
            right.push(n)
        }
    }

    return quickSort1(left).concat(
        [midValue],
        quickSort1(right)
    )
}

/**
 * 快速排序（使用 slice）
 * @param arr number arr
 */
export function quickSort2(arr: number[]): number[] {
    const length = arr.length
    if (length === 0) return arr

    const midIndex = Math.floor(length / 2)
    const midValue = arr.slice(midIndex, midIndex + 1)[0]

    const left: number[] = []
    const right: number[] = []

    for (let i = 0; i < length; i++) {
        if (i !== midIndex) {
            const n = arr[i]
            if (n < midValue) {
                // 小于 midValue ，则放在 left
                left.push(n)
            } else {
                // 大于 midValue ，则放在 right
                right.push(n)
            }
        }
    }

    return quickSort2(left).concat(
        [midValue],
        quickSort2(right)
    )
}

// // 功能测试
const arr1 = [1, 6, 2, 7, 3, 8, 4, 9, 5]
console.info(quickSort2(arr1))

// // 性能测试
// const arr1 = []
// for (let i = 0; i < 10 * 10000; i++) {
//     arr1.push(Math.floor(Math.random() * 1000))
// }
// console.time('quickSort1')
// quickSort1(arr1)
// console.timeEnd('quickSort1') // 74ms

// const arr2 = []
// for (let i = 0; i < 10 * 10000; i++) {
//     arr2.push(Math.floor(Math.random() * 1000))
// }
// console.time('quickSort2')
// quickSort2(arr2)
// console.timeEnd('quickSort2') // 82ms

// // 单独比较 splice 和 slice
// const arr1 = []
// for (let i = 0; i < 10 * 10000; i++) {
//     arr1.push(Math.floor(Math.random() * 1000))
// }
// console.time('splice')
// arr1.splice(5 * 10000, 1)
// console.timeEnd('splice')
// const arr2 = []
// for (let i = 0; i < 10 * 10000; i++) {
//     arr2.push(Math.floor(Math.random() * 1000))
// }
// console.time('slice')
// arr2.slice(5 * 10000, 5 * 10000 + 1)
// console.timeEnd('slice')

1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151, 161, 171, 181, 191

1-10000 之间的对称数（回文）

题目
- 打印 1-10000 之间的对称数
- 11, 22, 33, 44, 55, 66, 77, 88, 99, 101, 111, 121, 131, 141, 151 (这些就是回文数字)
思路1：使用数组反转
- 数字转换为字符串
- 字符串转换为数组 reverse ，再 join 生成字符串
- 比较前后的字符串
思路2：使用字符串头尾比较
- 数字转换为字符串
- 字符串头尾比较
- 还可以使用栈（但栈会用到数组，性能不如直接操作字符串）
  - 数字转换为字符串，求长度
  - 如果长度是偶数，则用栈比较
  - 如果长度是奇数，则忽略中间的数字，其他的用栈比较
思路3：生成反转数
- 通过 % 和 Math.floor 将数字生成一个反转数
- 比较前后的数字
性能分析
时间复杂度看似相当，都是 O(n)
- 思路1
  - 涉及到了数组的转换和操作，就需要耗费大量的时间
  - 数组 reverse 需要时间
  - 数组和字符串的转换需要时间
- 思路2/3
  - 数字操作最快。电脑的原型就是计算器，所以处理数字是最快的。

/**
 * @description 对称数
 */

/**
 * 查询 1-max 的所有对称数（数组反转）
 * @param max 最大值
 */
export function findPalindromeNumbers1(max: number): number[] {
    const res: number[] = []
    if (max <= 0) return res

    for (let i = 1; i <= max; i++) {
        // 转换为字符串，转换为数组，再反转，比较
        const s = i.toString()
        if (s === s.split('').reverse().join('')) {
            res.push(i)
        }
    }

    return res
}

/**
 * 查询 1-max 的所有对称数（字符串前后比较）
 * @param max 最大值
 */
export function findPalindromeNumbers2(max: number): number[] {
    const res: number[] = []
    if (max <= 0) return res

    for (let i = 1; i <= max; i++) {
        const s = i.toString()
        const length = s.length

        // 字符串头尾比较
        let flag = true
        let startIndex = 0 // 字符串开始
        let endIndex = length - 1 // 字符串结束
        while (startIndex < endIndex) {
            if (s[startIndex] !== s[endIndex]) {
                flag = false
                break
            } else {
                // 继续比较
                startIndex++
                endIndex--
            }
        }

        if (flag) res.push(i)
    }

    return res
}

/**
 * 查询 1-max 的所有对称数（翻转数字）
 * @param max 最大值
 */
export function findPalindromeNumbers3(max: number): number[] {
    const res: number[] = []
    if (max <= 0) return res

    for (let i = 1; i <= max; i++) {
        let n = i
        let rev = 0 // 存储翻转数

        // 生成翻转数
        while (n > 0) {
            rev = rev * 10 + n % 10
            n = Math.floor(n / 10)
        }

        if (i === rev) res.push(i)
    }

    return res
}


// 功能测试
// console.info(findPalindromeNumbers3(200))

// 性能测试
console.time('findPalindromeNumbers1')
findPalindromeNumbers1(100 * 10000)
console.timeEnd('findPalindromeNumbers1') // 408ms

console.time('findPalindromeNumbers2')
findPalindromeNumbers2(100 * 10000)
console.timeEnd('findPalindromeNumbers2') // 53ms

console.time('findPalindromeNumbers3')
findPalindromeNumbers3(100 * 10000)
console.timeEnd('findPalindromeNumbers3') // 42ms

搜索单词 - 字符串前缀匹配

题目
- 请描述算法思路，不要求写出代码。
  - 先给一个英文单词库（数组），里面有几十万个英文单词
  - 再给一个输入框，输入字母，搜索单词
  - 输入英文字母，要实时给出搜索结果，按前缀匹配
- 要求
  - 尽量快
  - 不要使用防抖（输入过程中就及时识别）
思路1：常规思路
- keyup 之后，拿当前的单词，遍历词库数组，通过 indexOf 来前缀匹配。

思路2：优化数据结构（Trie 树（字典树））

英文字母一共 26 个，可按照第一个字母分组，分为 26 组。这样搜索次数就减少很多。
可按照第二个、第三个字母分组。
即，在程序初始化时，把数组变成一个树，然后按照字母顺序在树中查找。

const arr = [
    'abs',
    'arab',
    'array',
    'arrow',
    'boot',
    'boss',
    // 更多...
]
const obj = {
    a: {
        b: {
            s: {}
        },
        r: {
            a: {
                b: {}
            },
            r: {
                a: {
                    y: {}
                },
                o: {
                    w: {}
                }
            }
        }
    },
    b: {
        o: {
            o: {
                t: {}
            },
            s: {
                s: {}
            }
        }
    },
    // 更多...
}

性能分析
- 思路1
  - 算法思路的时间复杂度是 O(n)
  - 外加 indexOf 也需要时间复杂度。实际的复杂度要超过 O(n)
- 思路2
  - 时间复杂度就大幅度减少，从 O(n) 降低到 O(m) （m 是单词的最大长度）
划重点
- 对于已经明确的范围的数据，可以考虑使用哈希表
- 以空间换时间

// 定义 Trie 节点接口
interface TrieNode {
  children: { [key: string]: TrieNode };
  isWord: boolean;
}

// 定义 Trie 类
export default class Trie {
  root: TrieNode;

  constructor() {
      this.root = {
          children: {},
          isWord: false
      };
  }

  insert(word: string): void {
      let node: TrieNode = this.root;
      for (const char of word) {
          if (!node.children[char]) {
              node.children[char] = {
                  children: {},
                  isWord: false
              };
          }
          node = node.children[char];
      }
      node.isWord = true;
  }

  search(prefix: string): string[] {
      let node: TrieNode = this.root;
      for (const char of prefix) {
          if (!node.children[char]) {
              return [];
          }
          node = node.children[char];
      }
      return this.collectWords(node, prefix);
  }

  private collectWords(node: TrieNode, prefix: string): string[] {
      const words: string[] = [];
      this.collectWordsHelper(node, prefix, words);
      return words;
  }

  private collectWordsHelper(node: TrieNode, currentWord: string, words: string[]): void {
      if (node.isWord) {
          words.push(currentWord);
      }

      for (const char in node.children) {
          if (node.children.hasOwnProperty(char)) {
              this.collectWordsHelper(node.children[char], currentWord + char, words);
          }
      }
  }
  private collectWords2(node: TrieNode, prefix: string): string[] {
    const words: string[] = [];
    const queue: { node: TrieNode; word: string }[] = [{ node: node, word: prefix }];

    while (queue.length > 0) {
        const { node: currentNode, word: currentWord } = queue.shift();

        if (currentNode.isWord) {
            words.push(currentWord);
        }

        for (const char in currentNode.children) {
            if (currentNode.children.hasOwnProperty(char)) {
                queue.push({ node: currentNode.children[char], word: currentWord + char });
            }
        }
    }

    return words;
}
}

// 示例用法
const wordList: string[] = ['abs', 'arab', 'array', 'arrow', 'boot', 'boss'];
const trie: Trie = new Trie();

for (const word of wordList) {
  trie.insert(word);
}

function searchWords(prefix: string): string[] {
  return trie.search(prefix);
}

// 搜索示例
console.log(searchWords('ar'));   // 输出: [ 'arab', 'array', 'arrow' ]
console.log(searchWords('bo'));   // 输出: [ 'boot', 'boss' ]
console.log(searchWords('a'));    // 输出: [ 'abs', 'arab', 'array', 'arrow' ]
console.log(searchWords('abc'));  // 输出: []

数字千分位

题目
- 将数字按照千分位生成字符串，即每三位加一个逗号。不考虑小数。
- 如输入数字 78100200300 返回字符串 '78,100,200,300'
思路
- 使用数组
- 使用正则表达式
- 使用字符串拆分
性能分析
- 数组转换，影响性能
- 正则表达式，性能较差
- 操作字符串，性能较好

/**
 * @description 千分位格式化
 */

/**
 * 千分位格式化（使用数组）
 * @param n number
 */
export function format1(n: number): string {
    n = Math.floor(n) // 只考虑整数

    const s = n.toString()
    const arr = s.split('').reverse()
    return arr.reduce((prev, val, index) => {
        if (index % 3 === 0) {
            if (prev) {
                return val + ',' + prev
            } else {
                return val
            }
        } else {
            return val + prev
        }
    }, '')
}

/**
 * 数字千分位格式化（字符串分析）
 * @param n number
 */
export function format2(n: number): string {
    n = Math.floor(n) // 只考虑整数

    let res = ''
    const s = n.toString()
    const length = s.length
    for (let i = length - 1; i >= 0; i--) {
        // 关键点：从后往前添加
        const j = length - i // j是动态的，length - i，实际上是倒着数第几个
        if (j % 3 === 0) {
            if (i === 0) { // 到达头部
                res = s[i] + res
            } else {
                res = ',' + s[i] + res
            }
        } else {
            res = s[i] + res
        }
    }

    return res
}

// // 功能测试
// const n = 10201004050
// console.info('format1', format1(n))
// console.info('format2', format2(n))

切换字母大小写

题目
- 切换字母大小写，输入 'aBc' 输出 'AbC'
思路
- 需要判断字母是大写还是小写
- 正则表达式
- charCodeAt 获取 ASCII 码（ASCII 码表，可以网上搜索）
性能分析
- 正则表达式性能较差
- ASCII 码性能较好

/**
 * @description 切换字母大小写
 */

/**
 * 切换字母大小写（正则表达式）
 * @param s str
 */
export function switchLetterCase1(s: string): string {
    let res = ''

    const length = s.length
    if (length === 0) return res

    const reg1 = /[a-z]/
    const reg2 = /[A-Z]/

    for (let i = 0; i < length; i++) {
        const c = s[i]
        if (reg1.test(c)) {
            res += c.toUpperCase()
        } else if (reg2.test(c)) {
            res += c.toLowerCase()
        } else {
            res += c
        }
    }

    return res
}

/**
 * 切换字母大小写（ASCII 编码）
 * @param s str
 */
export function switchLetterCase2(s: string): string {
    let res = ''

    const length = s.length
    if (length === 0) return res

    for (let i = 0; i < length; i++) {
        const c = s[i]
        const code = c.charCodeAt(0)

        if (code >= 65 && code <= 90) {
            res += c.toLowerCase()
        } else if (code >= 97 && code <= 122) {
            res += c.toUpperCase()
        } else {
            res += c
        }
    }

    return res
}

// // 功能测试
// const str = '100aBcD$#xYz'
// console.info(switchLetterCase2(str))

// // 性能测试
// const str = '100aBcD$#xYz100aBcD$#xYz100aBcD$#xYz100aBcD$#xYz100aBcD$#xYz100aBcD$#xYz'
// console.time('switchLetterCase1')
// for (let i = 0; i < 10 * 10000; i++) {
//     switchLetterCase1(str)
// }
// console.timeEnd('switchLetterCase1') // 436ms

// console.time('switchLetterCase2')
// for (let i = 0; i < 10 * 10000; i++) {
//     switchLetterCase2(str)
// }
// console.timeEnd('switchLetterCase2') // 210ms

遍历 DOM 树

题目
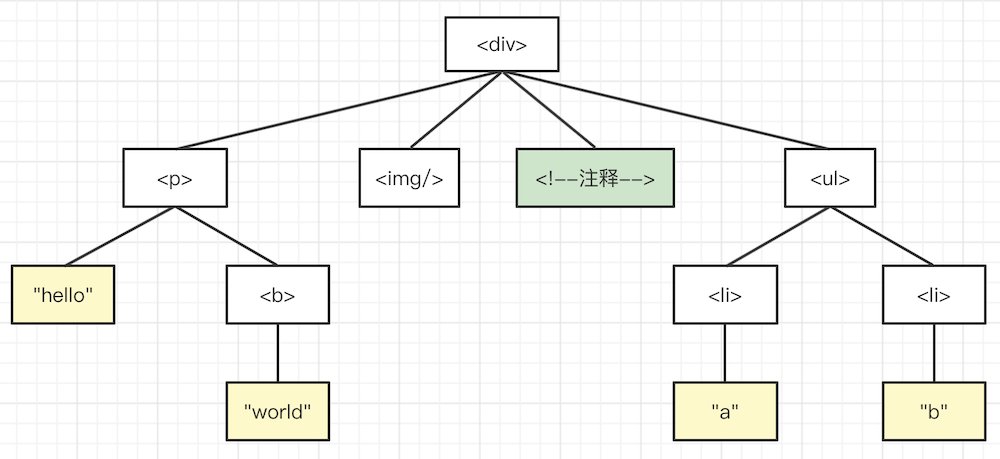
- 写一个函数遍历 DOM 树，分别用深度优先和广度优先
- 注意回顾 “Node 和 Element 和区别”
思路
- 深度优先
  - 一般通过递归实现
  - 递归：就递归遍历子节点，便利执行这个动作，直到没有子节点为止。
  - 深度优先的结果 <div> <p> "hello" <b> "world" <img> 注释 <ul> <li> "a" <li> "b"
  - 深度优先遍历，可以使用栈代替递归，递归本质上就是栈。(深度优先可以不用递归吗？)
  - 栈：获取当前节点，子节点反转再遍历，子节点push入栈，在将栈中的节点pop出栈，重复这个过程。(保证左子节点一直处于栈顶，达到深度优先)
- 广度优先
  - 一般通过队列实现
  - 队列：获取当前节点，便利子节点，子节点unshift入队列头部，在将队列中的节点pop出队列尾部，重复这个过程。（保证统一层级的节点最先遍历）
  - 广度优先的结果 <div> <p> <img> 注释 <ul> "hello" <b> <li> <li> "world" "a" "b"
划重点
- 递归和非递归哪个更好？
- 递归逻辑更加清晰，但容易出现 stack overflow 错误（可使用尾递归，编译器有优化）
- 非递归效率更高，但使用栈，逻辑稍微复杂一些

/**
 * @description 遍历 DOM tree
 */

/**
 * 访问节点
 * @param n node
 */
function visitNode(n: Node) {
    if (n instanceof Comment) {
        // 注释
        console.info('Comment node ---', n.textContent)
    }
    if (n instanceof Text) {
        // 文本
        const t = n.textContent?.trim()
        if (t) {
            console.info('Text node ---', t)
        }
    }
    if (n instanceof HTMLElement) {
        // element
        console.info('Element node ---', `<${n.tagName.toLowerCase()}>`)
    }
}

/**
 * 深度优先遍历
 * @param root dom node
 */
function depthFirstTraverse1(root: Node) {
    visitNode(root)

    const childNodes = root.childNodes // .childNodes 和 .children 不一样
    if (childNodes.length) {
        childNodes.forEach(child => {
            depthFirstTraverse1(child) // 递归
        })
    }
}

/**
 * 深度优先遍历
 * @param root dom node
 */
 function depthFirstTraverse2(root: Node) {
     const stack: Node[] = []

     // 根节点压栈
     stack.push(root)

     while (stack.length > 0) {
         const curNode = stack.pop() // 出栈
         if (curNode == null) break

         visitNode(curNode)

         // 子节点压栈
         const childNodes = curNode.childNodes
         if (childNodes.length > 0) {
             // reverse 反顺序压栈
             Array.from(childNodes).reverse().forEach(child => stack.push(child))
         }
     }
 }

/**
 * 广度优先遍历
 * @param root dom node
 */
function breadthFirstTraverse(root: Node) {
    const queue: Node[] = [] // 数组 vs 链表

    // 根节点入队列
    queue.unshift(root)

    while (queue.length > 0) {
        const curNode = queue.pop()
        if (curNode == null) break

        visitNode(curNode)

        // 子节点入队
        const childNodes = curNode.childNodes
        if (childNodes.length) {
            childNodes.forEach(child => queue.unshift(child))
        }
    }
}

const box = document.getElementById('box')
if (box == null) throw new Error('box is null')
depthFirstTraverse2(box)

算法 ​

复杂度 ​

时间复杂度 ​

空间复杂度 ​

算法思维 ​

贪心 ​

二分 ​

动态规划 ​

数据结构 ​

栈 Stack ​

队列 Queue ​

链表 Linked List ​

树 ​

二叉搜索树 BST ​

堆 ​

性能 ​

题目 ​

旋转数组 ​

括号匹配 ​

用两个栈实现一个队列 ​

反转单向链表 ​

二分查找 ​

两数之和 ​

求二叉搜索树的第 K 小的值 ​

斐波那契数列 &I ​

青蛙跳台阶 ​

移动 0 ​

连续最多的字符 ​

快速排序 &I ​

1-10000 之间的对称数（回文） ​

搜索单词 - 字符串前缀匹配 ​

数字千分位 ​

切换字母大小写 ​

遍历 DOM 树 ​

算法

复杂度

时间复杂度

空间复杂度

算法思维

贪心

二分

动态规划

数据结构

栈 Stack

队列 Queue

链表 Linked List

树

二叉搜索树 BST

堆

性能

题目

旋转数组

括号匹配

用两个栈实现一个队列

反转单向链表

二分查找

两数之和

求二叉搜索树的第 K 小的值

斐波那契数列 &I

青蛙跳台阶

移动 0

连续最多的字符

快速排序 &I

1-10000 之间的对称数（回文）

搜索单词 - 字符串前缀匹配

数字千分位

切换字母大小写

遍历 DOM 树